算法衡量优劣之时间复杂度

共计 4734 个字符，预计需要花费 12 分钟才能阅读完成。

选型

我们假定计算机执行算法每一个基本操作的时间是固定的一个时间单位 , 那么有多少个基本操作就代表会花费多少时间单位 , 由此可以忽略机器环境的影响而客观的反应算法的时间效率

代码执行总时间(T) = 操作步骤数量 * 操作步骤执行时间（忽略机器环境的影响）

算法时间复杂度是用来描述算法在运行时所需的时间资源的度量。它通常表示为一个函数，该函数描述了算法的运行时间与输入规模之间的关系。

时间复杂度是分析算法性能的重要工具，它可以帮助我们比较不同算法的效率，以便在解决问题时选择最优算法。

时间复杂度通常使用大 O 符号（O）来表示，以下是一些常见的时间复杂度：

1. O(1) – 常数时间复杂度：算法的运行时间与输入规模无关，即使输入规模增加，运行时间也保持不变。例如，访问数组的某个元素（通过索引访问）。
   • 示例：访问数组中的元素、插入或删除链表的头节点。
   • 最佳实践：常数时间复杂度是最理想的情况，尽量选择常数时间的算法。
2. O(log n) – 对数时间复杂度：算法的运行时间与输入规模的对数成正比。典型示例是二分查找。
   • 示例：二分查找、某些分治算法。
   • 最佳实践：对数时间复杂度通常表示算法在大规模数据上具有很好的性能，尤其在搜索和排序问题上。
3. O(n) – 线性时间复杂度：算法的运行时间与输入规模成线性关系。例如，遍历数组中的所有元素。
   • 示例：遍历数组、查找未排序的数组中的元素。
   • 最佳实践：线性时间复杂度是一种常见的时间复杂度，通常是一个合理的选择。但对于某些问题，可能需要更高效的算法。
4. O(n log n) – 线性对数时间复杂度：算法的运行时间与输入规模的线性关系乘以对数。典型示例是快速排序和归并排序。
   • 示例：快速排序、归并排序、某些高效的搜索算法。
   • 最佳实践：线性对数时间复杂度通常是排序问题的最佳选择，它在大规模数据上表现出色。
5. O(n^2) – 平方时间复杂度：算法的运行时间与输入规模的平方成正比。例如，嵌套循环遍历二维数组。
   • 示例：冒泡排序、插入排序、某些矩阵运算。
   • 最佳实践：平方时间复杂度通常在大规模问题上表现较差，尽量避免使用，除非输入规模非常小。
6. O(n^k) – 多项式时间复杂度：算法的运行时间与输入规模的幂次成正比，其中 k 是常数。例如，一些多项式时间复杂度的动态规划算法。
   • 示例：某些动态规划算法。
   • 最佳实践：多项式时间复杂度通常在问题的解空间较大时表现较好，但需要权衡计算时间和内存消耗。
7. O(2^n) – 指数时间复杂度：算法的运行时间与输入规模的指数成正比。典型示例是解决旅行推销员问题的暴力搜索。
   • 示例：旅行推销员问题的穷举法解法。
   • 最佳实践：指数时间复杂度通常在大规模问题上不可接受，需要寻找更高效的算法。
8. O(n!) – 阶乘时间复杂度：算法的运行时间与输入规模的阶乘成正比。典型示例是解决旅行推销员问题的穷举法。
   • 示例：旅行推销员问题的穷举法解法。
   • 最佳实践：阶乘时间复杂度通常在实际问题中不可接受，需要考虑其他解决方案。

常见时间复杂度的对比：

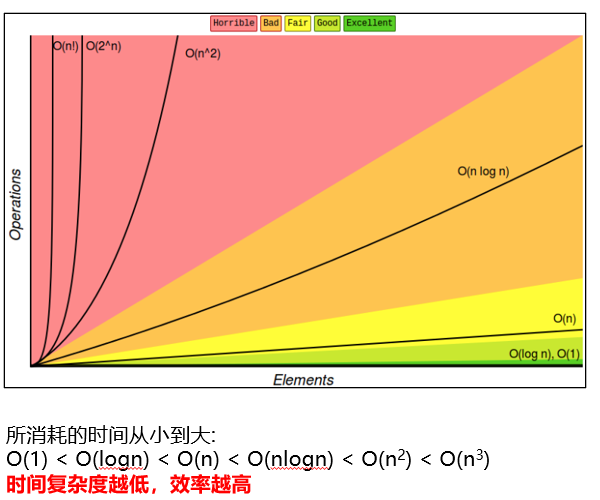
最佳实践：

1. 问题分析：在选择时间复杂度时，首先仔细分析问题的性质和输入规模，以确定哪种时间复杂度最合适。
2.  选择合适的数据结构：选择适合问题的数据结构可以显著影响算法的时间复杂度。例如，对于查找操作，哈希表通常比线性搜索更快。
3. 选择经典算法：考虑使用已知的高效算法，避免自行实现复杂的算法，除非必要。特别是在问题领域已经有成熟的解决方案时。
4. 性能测试：对不同时间复杂度的算法进行性能测试，以确定哪种算法在实际应用中表现最佳。
5. 优化：对于高时间复杂度的算法，考虑优化方案，例如使用更快的数据结构、剪枝、并行化等。
6.  避免不必要的操作：精简算法以减少不必要的操作，以降低时间复杂度。考虑是否可以剪枝、合并循环等。
7. 平衡：在选择时间复杂度时，需要平衡算法的运行时间和内存消耗。有时候，降低时间复杂度可能会导致更高的内存使用。
8. 维护和测试：定期维护和测试算法，确保它在不同场景下仍然高效。
9.  分析和测试：对算法进行时间复杂度分析，并进行实际测试来验证性能。确保算法在不同规模的输入下都能有效运行。

示例：让我们看一个示例，计算前 n 个自然数的和的算法，并分析它的时间复杂度。

1 def sum_of_n_natural_numbers(n):
2     total = 0
3     for i in range(1, n + 1):
4         total += i
5     return total

坑：

1. 忽略常数因子：时间复杂度分析通常忽略常数因子。因此，O(2n) 和 O(n) 在大规模问题上被认为是相同的。
2. 不同情况下的时间复杂度：算法的时间复杂度可能在不同情况下有所不同，例如最佳情况、最坏情况和平均情况。需要考虑这些情况来全面评估算法性能。
3. 空间复杂度：时间复杂度只关注运行时间，而不考虑内存消耗。要考虑算法的空间复杂度，特别是对于内存有限的环境。

最优、最坏、平均时间复杂度为啥选最坏时间复杂度？     

    对于最优时间复杂度，其价值不大，因为它没有提供什么有用信息其反映的只是最乐观最理想的情况，没有参考价值。   

    对于最坏时间复杂度，提供了一种保证，表明算法在此种程度的基本操作中一定能完成工作 。

    对于平均时间复杂度，是对算法的一个全面评价，因此它完整全面 的反映了这个算法的性质。但另一方面，这种衡量并没有保证，不 是每个计算都能在这个基本操作内完成。而且，对于平均情况的计

算，也会因为应用算法的实例分布可能并不均匀而难以计算。

因此，我们主要关注算法的最坏情况，亦即最坏时间复杂度

时间复杂度的计算规则:

①基本操作，认为其时间复杂度为 O(1)
②顺序结构，时间复杂度按加法进行计算
③循环结构，时间复杂度按乘法进行计算
④分支结构，时间复杂度取最大值(哪个分支的时间复杂度大，去那个)
⑤判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略
⑥在没有特殊说明时，我 们所分析的算法的时间复杂度都是指最坏时间复杂度

优化

以一个题目讲解时间复杂度的优化：    选型：使用穷尽法。在此选型的基础上做代码优化（题目分析 + 用对数据结构 + 减少遍历 + 数学基础）

如果 a+b+c=1000，且 a^2+b^2=c^2（a,b,c 为自然数），如何求出所有 a、b、c 可能的组合?

  方法 1：直接穷举法（不伤脑）

import time

'''
方法一：穷举法
这是一种最简单的方法，它穷尽了所有可能的自然数三元组，检查是否满足条件。'''


def find_pythagorean_triplets01(n):
    triplets = []  # 定义一个列表存放满足条件的结果
    n = n + 1
    for a in range(0, n):
        for b in range(0, n):  # 因为自然数是包括 0 的
            for c in range(0, n):
                if a ** 2 + b ** 2 == c ** 2 and (a + b + c == n - 1):
                    triplets.append((a, b, c))
    return triplets


def find_pythagorean_triplets02(n):
    triplets = []
    n = n + 1
    for a in range(1, n):
        for b in range(a, n):
            c = n-1 - a - b
            if a ** 2 + b ** 2 == c ** 2:
                triplets.append((a, b, c))
    return triplets


# 记录开始时间
start_time = time.time()
triplets = find_pythagorean_triplets01(1000)
# 记录结束时间
end_time = time.time()
# 计算执行时间
execution_time = end_time - start_time
# 打印执行时间
print(f"find_pythagorean_triplets01 方法执行时间: {execution_time} 秒")
print(f"find_pythagorean_triplets01 方法执行结果:{triplets}")

  输出结果：

O(n^3)

方法 2：优化的穷举法

1 import time
 2 
 3 def find_pythagorean_triplets02(n):
 4     triplets = []
 5     n = n + 1
 6     for a in range(0, n):
 7         # for b in range(a, n):  # 此处考虑去重
 8         for b in range(0, n):  # 不去重使用此处
 9             c = n-1 - a - b
10             if a ** 2 + b ** 2 == c ** 2:
11                 triplets.append((a, b, c))
12     return triplets
13 
14 # 记录开始时间
15 start_time = time.time()
16 triplets = find_pythagorean_triplets02(1000)
17 # 记录结束时间
18 end_time = time.time()
19 # 计算执行时间
20 execution_time = end_time - start_time
21 # 打印执行时间
22 print(f"find_pythagorean_triplets01 方法执行时间: {execution_time} 秒")
23 print(f"find_pythagorean_triplets01 方法执行结果:{triplets}")

输出：

去重时限制了 b 的取值范围，避免了不必要的迭代。避免一次循环（相对不伤脑）

从输出结果上看看，优化后耗时很 nice（1000 倍）

方法 3：数学优化（去重，不包括 0）

1 import time
 2 
 3 # 方法 3: 数学推理优化
 4 def find_pythagorean_triplets03():
 5     triplets = []
 6     for a in range(1, 1000):
 7         b = (500000 - 1000 * a) / (1000 - a)
 8         if b.is_integer() and b > 0:
 9             c = 1000 - a - int(b)
10             triplets.append((a, int(b), c))
11     return triplets
12 
13 
14 
15 
16 # 记录开始时间
17 start_time = time.time()
18 triplets = find_pythagorean_triplets03()
19 # 记录结束时间
20 end_time = time.time()
21 # 计算执行时间
22 execution_time = end_time - start_time
23 # 打印执行时间
24 print(f"find_pythagorean_triplets01 方法执行时间: {execution_time} 秒")
25 print(f"find_pythagorean_triplets01 方法执行结果:{triplets}")

输出：

find_pythagorean_triplets01 方法执行时间: 0.0 秒
find_pythagorean_triplets01 方法执行结果:[(200, 375, 425), (375, 200, 425)]

这速度也没谁了。

虽然方法 1 到方法 3 没有增加数据量，但优化的结果，在时间执行上，节约很多成本。